진행하는 과정에서 생길 수 있는 부분에 대해서는
Q.라고 적어두고 하단부에 모두 설명할 테니 참고하자.
개념
주어진 데이터의 구간 합과 데이터 업데이트를 빠르게 수행하기 위해 고안해낸 자료구조의 형태가 바로 세그먼트 트리이다.
더 큰 범위는 '인덱스 트리'라고 불린다.
1차원 배열에서의 구간합 저장 배열을 이용하는 것보다 복잡한 과정을 거치지만, 업데이트가 발생하는 경우 효율적인 성능을 발휘한다.
Q. 데이터 업데이트가 왜 빠른가요?
Q. 구간 곱, 최대 최소 탐색에는 어떻게 활용하나요?
세그먼트 트리 수행 과정
우리는 {3, 1, 4, 1, 5, 9, 2, 6} 배열의 구간합을 예시로 세그먼트 트리를 이해해 볼 것이다.

우리가 구간합을 구하고자 하는 배열을 생각해보자. 총 8개의 숫자로 구성된 배열이다. 이를 이진트리의 최하단부에 넣을 것이다.
여기서 첫번째 규칙이 나온다.
1. 2^k >= n을 만족시키는 최소의 k를 찾는다.
2. 배열의 크기를 2^(k+1)로 만든다.
3. 주어진 숫자를 2^k부터 넣는다.
무슨 소리일까? 일단 규칙을 맘에 넣어두고, 과정을 따라가 보자.
1. n = 8이기 때문에 k = 3이 될 것이다.
2. 배열의 크기를 2^4 = 16으로 선언하자.
3. 주어진 숫자를 2^3 = 8부터 넣자. -> 완성된 배열을 보자.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 3 | 1 |
| 10 | 11 | 12 | 13 | 14 | 15 |
| 4 | 1 | 5 | 9 | 2 | 6 |
위와 같은 배열을 완성할 수 있다.
Q. 만약 뒷부분이 남으면 어떻게 하나요?
이진트리에서의 인덱스는 부모노드가 x라고 했을 때, 2x와 2x+1이다. -> 이진트리의 규칙이다. 하단의 인덱스를 갖는 그림으로 완성된다.

이제 두 번째 규칙이 나온다.
4. 끝에서부터 idx/2 자리에 자신의 값을 추가한다.
그 과정을 따라가 보자. 모든 과정을 배열로 보기엔 복잡하니, 문장으로 적고 아래 완성하겠다.
1. idx : 15일 때 -> segment[15/2] += segment[15]
2. idx : 14일 때 -> segment[14/2] += segment[14]
3. idx : 13일 때 -> segment[13/2] += segment[13]
4. idx : 12일 때 -> segment[12/2] += segment[12]
5. idx : 11일 때 -> segment[11/2] += segment[11]
6. idx : 10일 때 -> segment[10/2] += segment[10]
7. idx : 9일 때 -> segment[9/2] += segment[9]
8. idx : 8일 때 -> segment[8/2] += segment[8]
9. idx : 7일 때 -> segment[7/2] += segment[7]
10. idx : 6일 때 -> segment[6/2] += segment[6]
11. idx : 5일 때 -> segment[5/2] += segment[5]
12. idx : 4일 때 -> segment[4/2] += segment[4]
13. idx : 3일 때 -> segment[3/2] += segment[3]
14. idx : 2일 때 -> segment[2/2] += segment[2]
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 31 | 9 | 22 | 4 | 5 | 14 | 8 | 3 | 1 |
| 10 | 11 | 12 | 13 | 14 | 15 |
| 4 | 1 | 5 | 9 | 2 | 6 |
최종적으로 인덱스 1은 모든 구간의 합인 31을 나타내게 된다!
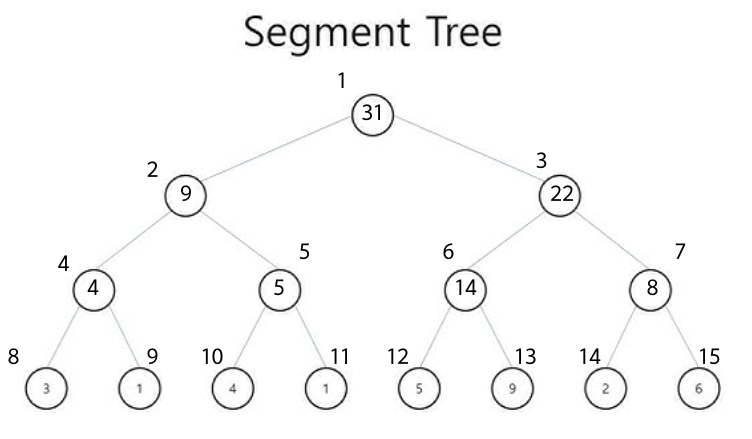
다음과 같이 세그먼트 트리가 완성됐다!
세그먼트 트리 질의 과정
이제 세그먼트 트리를 완성했으니 질의는 어떻게 하면 되는 걸까?

다시 이 트리를 살펴보자.
부모노드는 자식노드 구간의 합이다.
예를 들어 노드4를 보면 8~9의 합이고, 노드2는 8~11의 합이고, 노드1은 8~15의 합이다.
아 그건 알겠는데.. 9~12까지 더하고 싶으면 어떻게 해야 할까??
과정을 이해하고 따라오자.
1. start += 2^k - 1을 하자. -> 여기서 -1은 시작 인덱스를 0부터 한 것인지 1부터 한 것인지에 따라 설정해 주면 된다.
ex) 1~n까지 숫자가 있다. -> -1 해줘야 함. 0~n까지 있다. -> -1 해줄 필요 없음.
2. end += 2^k - 1을 하자. -> 위와 마찬가지다.
3. start % 2 == 1이면 노드를 선택하고, start += 1을 한다.
4. end % 2 == 0이면 노드를 선택하고, end -= 1을 한다.
5. start /= 2, end /= 2를 한다.
6. start <= end까지 3~5를 반복한다.
자! 이제 {3, 1, 4, 1, 5, 9, 2, 6}에서 2~5의 합을 구하여라. 의 문제를 직접 풀어보자.
1. 인덱스가 1부터 시작하는 것이니 start += 2^3 - 1 = 9
2. 인덱스가 1부터 시작하는 것이니 end += 2^3 - 1 = 12이다.
3. 9 % 2 == 1이다. 9번 노드를 선택한다. start += 1로 start = 10이 된다.
선택된 노드 : [9]
4. 12 % 2 == 0이다. 12번 노드를 선택한다. end -= 1로 end = 11이 된다.
선택된 노드 : [9, 12]
5. start = 5, end = 5가 된다.
6. start <= end 이므로 3으로 돌아간다.
7. 5 % 2 == 1이다. 5번 노드를 선택한다. start += 1로 start = 6이 된다.
선택된 노드 : [9, 12, 5]
8. 5 % 2 == 1이다. 5번 노드를 선택하지 않는다.(end % 2 == 0을 선택하기 때문) end = 5로 유지된다.
9. start = 3, end = 2가 된다.
10. 끝난다.
최종 선택된 노드를 보자. 9, 5, 12이다. 세 노드의 합이 2~5의 구간합이라는 것에 동의하는가? 트리를 살펴보면 동의가 될 것이다.
그럼 과정을 분석해 보자.
start % 2 == 1이라는 것은 자식 노드의 오른쪽이라는 것이다. start의 경우 같은 자식 노드인 왼쪽을 무시해야 한다는 말이다. 즉, 해당 노드를 선택해 주고, start += 1을 함으로써 자신의 부모 노드가 아닌 오른쪽 위 부모 노드로 이동하게 만들자.
end % 2 == 0이라는 것은 자식 노드의 왼쪽이라는 것이다. end의 경우 같은 자식 노드의 오른쪽을 무시해야한다는 말이다. 즉, 해당 노드를 선택해주고, end -= 1을 함으로써 자신의 부모노드가 아닌 왼쪽 위 부모노드로 이동하게 만들자.
최고 부모 인덱스가 1이기 때문에 최종적으로 start % 2 == 1에 걸리게 되어 합에 들어간다.
코드 구현
import java.io.*;
import java.util.*;
public class Main {
static long[] segmentTree;
static int squareNum;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
st = new StringTokenizer(br.readLine());
int n = Integer.parseInt(st.nextToken()); // 수의 개수
int m = Integer.parseInt(st.nextToken()); // 수의 변경이 일어나는 횟수
int k = Integer.parseInt(st.nextToken()); // 구간 합을 구하는 횟수
int square = 0; // 2^k >= n 을 만족하기 위한 수
while(Math.pow(2, square) < n){
square++;
}
squareNum = (int)Math.pow(2, square);
segmentTree = new long[(int)Math.pow(2,square+1)]; // 2^k * 2로 배열 초기화
for(int i = squareNum; i < squareNum + n; i++){
segmentTree[i] = Long.parseLong(br.readLine()); // 2^k 부터 값 저장.
}
for(int i = squareNum * 2 - 1; i >= 2; i--){
segmentTree[i/2] += segmentTree[i];
}
for(int i = 0; i < m + k; i++){
st = new StringTokenizer(br.readLine());
int command = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
long c = Long.parseLong(st.nextToken());
if(command == 1){
change(b, c);
continue;
}
if(command == 2){
System.out.println(query(b, (int) c));
}
}
}
static long query(int start, int end) {
start += squareNum - 1; // 리프 노드 시작 인덱스로 이동
end += squareNum - 1;
long sum = 0;
while (start <= end) {
// start가 오른쪽 자식이면 해당 노드 포함 후, 다음 노드로 이동
if (start % 2 == 1) {
sum += segmentTree[start];
start++;
}
// end가 왼쪽 자식이면 해당 노드 포함 후, 이전 노드로 이동
if (end % 2 == 0) {
sum += segmentTree[end];
end--;
}
// 부모 노드로 이동
start /= 2;
end /= 2;
}
return sum;
}
static void change(int changePoint, long changeNum){
changePoint += squareNum - 1;
long diff = changeNum - segmentTree[changePoint];
segmentTree[changePoint] = changeNum;
changePoint /= 2;
while(changePoint > 0){
segmentTree[changePoint] += diff;
changePoint /= 2;
}
}
}
백준-2042 https://www.acmicpc.net/problem/2042 의 풀이이다. 이를 이용하여 코드를 분석해보자.
int square = 0; // 2^k >= n 을 만족하기 위한 수
while(Math.pow(2, square) < n){
square++;
}
squareNum = (int)Math.pow(2, square);squaer를 먼저 구한 뒤 squareNum을 구한다. 이는 인덱스를 자리에 맞게 배치해주는 역할을 하게 된다.
segmentTree = new long[(int)Math.pow(2,square+1)]; // 2^k * 2로 배열 초기화
for(int i = squareNum; i < squareNum + n; i++){
segmentTree[i] = Long.parseLong(br.readLine()); // 2^k 부터 값 저장.
}
for(int i = squareNum * 2 - 1; i >= 2; i--){
segmentTree[i/2] += segmentTree[i];
}배열의 크기를 2^(k+1)의 사이즈로 초기화 한다. 이후 2^k위치부터 입력을 받아 배치한다.
나머지 앞부분 인덱스에 대해서는 끝에서부터 [idx/2]에 위치에 값을 저장하는 방식으로 채워나간다.
나머지 쿼리와 체인지 부분은 위에서 정리된 규칙을 코드로 구현한 것 뿐이다.
Q&A
Q. 데이터 업데이트가 왜 빠른가요?
A. 만약 길이가 n인 배열에 대해 합배열을 지정해 둔 경우 인덱스 2에 대해 변경을 가하게 되면 2~n까지 모두 수정을 해주어야 합니다. 이 경우 최대 O(N)의 시간복잡도를 요구합니다. 하지만 세그먼트 트리의 경우 O(logN)으로 최적의 업데이트를 보장합니다.
Q. 구간 곱, 최대 최소 탐색에는 어떻게 활용하나요?
A. 수행과정의 4번. 끝에서부터 idx/2 자리에 자신의 값을 추가한다. 이 파트를 원하는 대로 수정하면 된다. segment[n/2] = Math.max(segment[n/2], segment[n]) 같은 방식을 하면 최대를, Math.min을 사용하면 최소를 그리고 곱을 이용하면 구간곱을 추적할 수 있다. 즉, 수행 과정을 원하는대로 변경해 주면 된다.
Q. 만약 뒷부분이 남으면 어떻게 하나요?
A. 이진트리를 완성하기 위한 과정으로 문제 조건에 맞는 임의값으로 채워 넣어주면 됩니다. 구간합의 경우 뒷부분은 가중치가 없어야 하므로 0을 저장하거나, 구간곱의 경우 곱을 기록하기 위해 1을 저장하는 방식을 사용하면 됩니다.
'문제 풀이 > 도구정리' 카테고리의 다른 글
| [도구정리] 위상정렬(Topological Sort) (2) | 2025.08.12 |
|---|---|
| [도구정리] 코딩테스트 EOF 입력 처리(JAVA) (1) | 2025.06.16 |
| [도구정리] 최소 신장 트리(MST) - 크루스칼(kruskal) 알고리즘 (0) | 2025.04.07 |
| [도구정리] 플로이드-와샬(Floyd-Warshall) 알고리즘 (0) | 2025.04.01 |
| [도구정리] Binary Search(이분탐색/이진탐색) (0) | 2025.03.13 |